HTML & CSS Deep Dive Part 2: Turing Completeness - What makes HTML and CSS Turing Complete?

This is the second part of a two-part series aimed at exploring HTML and CSS in greater depth. Here’s the previous blog post where we go into the parsing and rendering of HTML and CSS.

In this blog post, we take a look at how a careful combination of markup and styling languages could possibly qualify as a computational system.

What are Turing Machines

A Turing machine is a mathematical model of computation describing an abstract machine that manipulates symbols on a strip of tape according to a table of rules. Despite the model’s simplicity, it is capable of implementing any computer algorithm.

Big words; let’s break it down.

Imagine an infinite strip of paper (called the tape) divided into small boxes. Each box can hold a symbol (like a letter or number).
There’s a robot (called the head) that moves along the tape. It can read what’s in a box, write something new, and move left or right.
The robot follows a set of rules (like a program). Based on what it reads and its current state, it decides what to do next.

This simple system can be used to simulate any computer program! Even though it’s very basic, it can solve any problem that a modern computer can—if given enough time and tape.

Here is a Turing machine that checks if an input string is a palindrome.

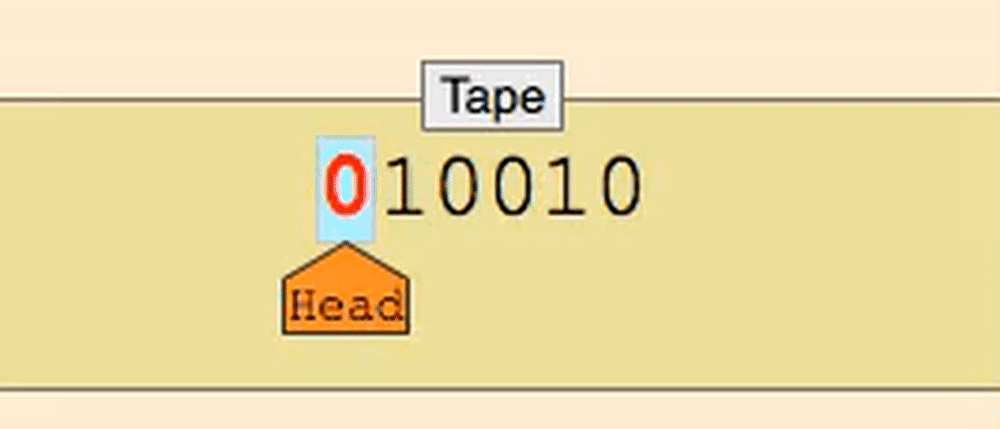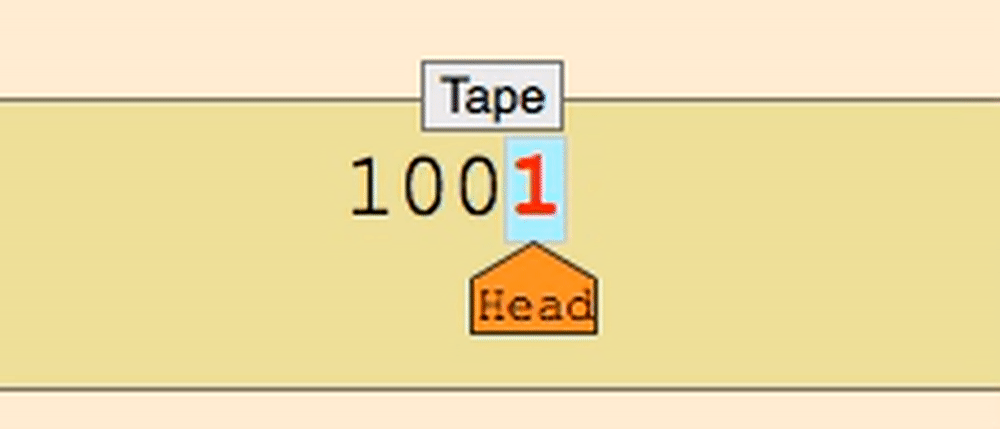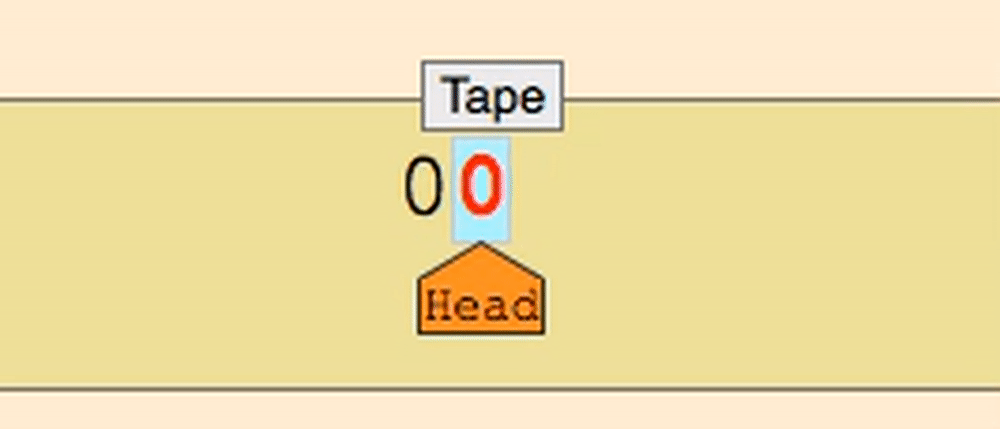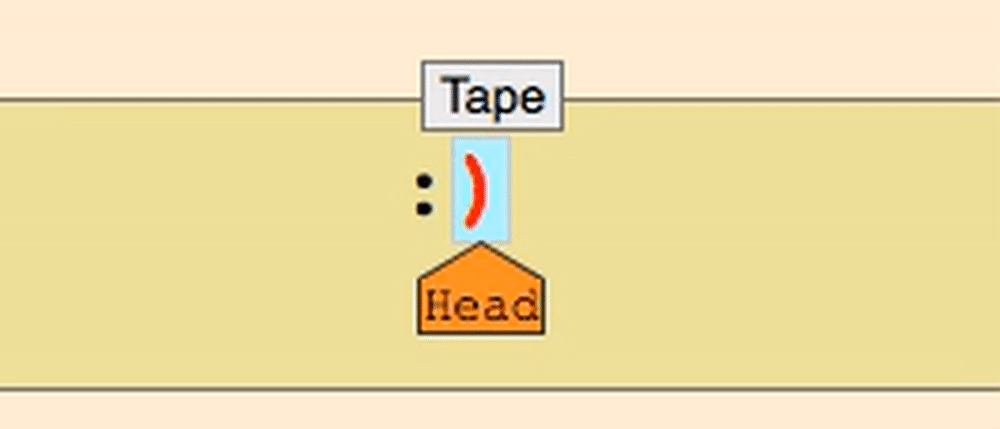
The tape head moves along the tape reading and writing symbols as directed by the Turing machine’s programming.

A Turing machine, like an algorithm, executes on an input string of bits. At the beginning, the input string is written on the tape, the tape head points to the first cell of the string, and all other cells are blank.

During operation, the tape head is in a certain state. Every step, it consults the table (the set of transition functions), based on only the state it’s in and the symbol underneath the head, to obtain its next choice: either halt (end the operation), or resume by writing a symbol to the current cell, changing its state, and moving to the left or the right. This way, A Turing machine can simulate the fact that a program is made of many lines and thus it depends on what line a program is executing, and it can also simulate the fact that a program can react differently with different data in memory.

When the tape reads any particular symbol, it decides what to do (what to write to the tape at that point and then which direction to move in next) depending on the set of transition functions associated with the machine. A transition function is essentially a specific instruction line in a Turing machine’s program. You can think of the set of transition functions as the complete program that specifies what the Turing machine should do on any valid input it receives.

What is “Turing Complete”

A computational system that can compute every Turing-computable function is called Turing-complete (or Turing-powerful). Alternatively, such a system is one that can simulate a universal Turing machine.

Again, let’s break it down -

A Turing-complete system is like a super-flexible computer— it can do anything that a Turing Machine can do, as long as it has enough time and memory.

Imagine a universal translator that can understand and speak any language.
A Turing-complete system is like that— it can run any possible computer program, no matter how complex.

Basically any system that meets the criteria of a Turing machine is considered Turing complete.

Let’s take an example.

The Rule 110 cellular automaton (often called simply Rule 110) is an elementary cellular automaton with interesting behavior on the boundary between stability and chaos. In this respect, it is similar to Conway’s Game of Life. Like Life, Rule 110 with a particular repeating background pattern is known to be Turing complete. This implies that, in principle, any calculation or computer program can be simulated using this automaton.

In an elementary cellular automaton, a one-dimensional pattern of 0s and 1s evolves according to a simple set of rules. Whether a point in the pattern will be 0 or 1 in the new generation depends on its current value, as well as on those of its two neighbors.

The Rule 110 automaton has the following set of rules:

Current pattern	111	110	101	100	011	010	001	000
New state for center cell	0	1	1	0	1	1	1	0

The name “Rule 110” derives from the fact that this rule can be summarized in the binary sequence 01101110; interpreted as a binary number, this corresponds to the decimal value 110. This is the Wolfram code naming scheme.

Why HTML and CSS Together are Turing Complete

The basic conditions for a Turing Machine are-

Arbitrary storage (memory) – The ability to store and retrieve an unlimited amount of information.
Conditional branching – The ability to make decisions (like if-else statements).
Loops (or recursion) – The ability to perform repeated computation indefinitely.

HTML and CSS alone lack explicit loops, conditionals, and memory. However, through creative abuse of CSS features, it is possible to construct a system that meets these requirements. That is where the magic lies ;)

Some researchers have shown that CSS alone (with carefully structured HTML) can simulate computation using clever hacks. Here’s how:

1. Memory Storage in CSS

CSS does not have traditional variables, but it does have a form of state storage using:

Counters (counter-reset, counter-increment)
Checkboxes and radio buttons (:checked states can hold information)
CSS animations (to control transitions between states)

By cleverly combining these, you can store and manipulate data.

2. Conditional Execution in CSS

CSS lacks if statements, but we can simulate conditionals using:

:checked pseudo-class (which changes styles based on user input)
:nth-child() selectors (which apply rules only to certain elements)
display: none and visibility: hidden (to selectively hide or show elements)

These allow CSS to make decisions based on user interactions or predefined states.

3. Loops & Computation in CSS

CSS does not have explicit loops, but infinite recursion can be simulated using animations:

CSS animations can be used to transition between states, effectively creating a looping mechanism.
Counters in CSS (counter-increment) can be incremented each time an element is re-rendered.
Recursive selector logic (e.g., nested nth-child rules) can create repeating structures.

These techniques enable CSS to simulate repeated execution, which is a key property of Turing completeness.

Let’s put these capabilities to test by implementing Rule 110 using plain HTML and CSS.

Pro Tip: This code is huge and repetitive. If you just want to see the concept (and keep your sanity), skip to the Codepen embed

body {
  -webkit-animation: bugfix infinite 1s;
  margin: 0.5em 1em;
}
@-webkit-keyframes bugfix {
  from {
    padding: 0;
  }
  to {
    padding: 0;
  }
}

/*
 * 111 110 101 100 011 010 001 000
 *  0   1   1   0   1   1   1   0
 */

body > input {
  -webkit-appearance: none;
  display: block;
  float: left;
  border-right: 1px solid #ddd;
  border-bottom: 1px solid #ddd;
  padding: 0px 3px;
  margin: 0;
  font-family: Consolas, "Courier New", monospace;
  font-size: 7pt;
}
body > input::before {
  content: "0";
}

p {
  font-family: Verdana, sans-serif;
  font-size: 9pt;
  margin-bottom: 0.5em;
}

body > input:nth-of-type(-n + 30) {
  border-top: 1px solid #ddd;
}
body > input:nth-of-type(30n + 1) {
  border-left: 1px solid #ddd;
  clear: left;
}

body > input::before {
  content: "0";
}

body > input:checked::before {
  content: "1";
}
body > input:checked {
  background: #afa !important;
}

/* 
the + selector applies by checking the state of 
adjacent cells to determine the next state 
*/

input:not(:checked)
  + *
  + *
  /* shrunk for brevity */
  + *
  + input::before {
  content: "1";
}
input:not(:checked)
  + *
  + *
  /* shrunk for brevity */
  + *
  + input {
  background: #fa0;
}

input:checked
  + *
  + *
  /* shrunk for brevity */
  + *
  + input::before {
  content: "1";
}
input:checked
  + *
  + *
  /* shrunk for brevity */
  + *
  + input {
  background: #fa0;
}

input:checked
  + *
  + *
  /* shrunk for brevity */
  + *
  + input::before {
  content: "1";
}
input:checked
  + *
  + *
  /* shrunk for brevity */
  + *
  + input {
  background: #fa0;
}

input:checked
  + input:checked
  + input:checked
  + *
  + *
  /* shrunk for brevity */
  + *
  + input::before {
  content: "0";
}
input:checked
  + input:checked
  + input:checked
  + *
  + *
  /* shrunk for brevity */
  + *
  + input {
  background: #fff;
}

input:not(:checked)
  + input:not(:checked)
  + input:not(:checked)
  + *
  + *
  /* shrunk for brevity */
  + *
  + input::before {
  content: "0";
}
input:not(:checked)
  + input:not(:checked)
  + input:not(:checked)
  + *
  + *
  /* shrunk for brevity */
  + *
  + input {
  background: #fff;
}

body > input:nth-child(30n) {
  display: none !important;
}
body > input:nth-child(30n) + label {
  display: none !important;
}

<!-- A total of 900 checkboxes required -->
<input type="checkbox" /><input type="checkbox" /><input
  type="checkbox"
/><input type="checkbox" /><input type="checkbox" /><input
  type="checkbox"
/><input type="checkbox" /><input type="checkbox" /><input
  type="checkbox"
/><input type="checkbox" /><input type="checkbox" /><input
  type="checkbox"
/><input type="checkbox" /><input type="checkbox" /><input
  type="checkbox"
/><input type="checkbox" />
<!-- 
 ...
 Shrunk for brevity
 ...
-->
<input type="checkbox" /><input type="checkbox" />

See the Pen HTML and CSS Rule 110 by Aditya Bhattacharya (Aditya Bhattacharya)

You can find a more elaborate (and correct) version of this example here. Continue reading to know why it is correct while the code given above quite isn’t.

But Is It Really?

The answer is… maybe. While a carefully crafted combination of HTML and CSS can emulate the implementation for Rule 110, it still does not qualify the very first condition - the input tape must be infinitely long. The interesting thing is, however, no modern computational system is Turing complete because physical memory is obviously finite (still). So any computational machine is still bound by practical limitations and technically isn’t Turing complete. And if we were to apply this same practical limitation on our smaller HTML and CSS scale, then it would qualify as Turing complete as well!

Our implementation also depends on user interaction in order to proceed or loop forward, so another point which can be raised is that only a well crafted HTML and CSS code incorporated with user interaction as a part of the CSS execution can qualify for Turing completeness.

This article goes into great detail on why our implementation of Rule 110 is still not Turing complete since it does not reach the dimensions required for Rule 110. However, the revamped version of this implementation is a complete implementation of Rule 110.

Ok, So What?

Let’s be honest— crafting Turing complete CSS is mostly a geeky curiosity or a “look what I can do!” challenge. Still, a few interesting points come out of this:

Educational Value: It showcases that what we consider “static” or “declarative” can be pushed to extremes if you find clever ways to store state and emulate logic. It’s a fascinating puzzle that sharpens our understanding of computation.
Fun & Comedic Examples: People have built pure CSS games (like the classic CSS-only “Frogger” or “Pac-Man”), purely to explore these boundaries. They highlight the “insanity factor” of pushing CSS beyond its intended scope.
Practical Use?: Outside of novel demos, not really. You’re far better off using JavaScript or other actual programming languages for real work. But if you want to prove a theoretical point or impress your developer friends, it’s a neat parlor trick.

Conclusion

In my opinion, the best way to conclude is one of my favorite comments on this debacle, by user Harmonic_Gear on Reddit -

desperately calling HTML a programming language is as silly as desperately classifying Pluto as planet, nobody cares

PS: Magic the Gathering is also Turing complete!

HTML & CSS Deep Dive Part 2: Turing Completeness of HTML and CSS